Andrea TRENTA, “Da Ipparco all’Intelligenza Artificiale, un percorso della conoscenza nella comprensione delle immagini”

ABSTRACT
Le conoscenze di cui oggi disponiamo per il riconoscimento delle immagini, alla base di molte applicazioni di A.I., dall’autenticazione biometrica alla guida autonoma, si sono accresciute nel corso dei secoli: riassumiamo alcune tappe del loro sviluppo per giungere a considerare alcune possibili evoluzioni degli standard ISO sulla qualità di prodotto.
Keywords: CNN, reti neurali, intelligenza artificiale, A.I., qualità dei dati, qualità del software, qualità del prodotto, nuove tecnologie, misure, ISO 25000.

Andrea TRENTA, Vicepresidente Commissione Tecnica CT 504 Ingegneria del Software UNINFO-SGI, andrea.trenta@dataqualitylab.it

---

Paper

Da Ipparco all’Intelligenza Artificiale: un percorso della conoscenza nella comprensione delle immagini 

I.       INTRODUZIONE  

Il percorso che ha portato all’attuale conoscenza sul riconoscimento delle immagini, alla base di molte applicazioni di A.I., dalla biometria ai veicoli a guida autonoma, si è sviluppato attraverso i secoli; vediamo nel seguito alcuni degli studiosi che hanno contribuito e gli aspetti principali con le relative implicazioni di matematica e geometria:

• ricostruzione della profondità in astronomia (Ipparco di Nicea)
• cartografia (Vitruvio)
• prospettiva (Guidobaldo del Monte)
• ricostruzione della profondità da immagini stereoscopiche (Cappeler)
• esaltazione dei contorni (Fourier)
• gli studi sulla corteccia visiva e le reti neurali artificiali, per cui ricordiamo tra molti studiosi, Yann LeCun.   

II.     3D E IL CALCOLO DELLA PROFONDITÀ: LA DISTANZA TERRA-LUNA DI IPPARCO DI NICEA

Ipparco utilizzò il metodo della parallasse, già usato da Aristarco di Samo circa un secolo prima, per determinare la distanza Terra-Luna, che gli consentì, successivamente, di stabilire la distanza tra la Terra e il Sole. Tale metodo, sfruttato dall’astronomo durante un’eclissi di sole nel 129 a.c., prevede che si osservi la posizione della Luna, contemporaneamente da due punti di vista differenti sulla Terra. Conoscendo che il Sole occupa circa 0,5° della volta celeste e che l’angolo alfa è 1\5 di =0,5° (perché durante l’eclisse di sole solo il 20% del sole è visibile da Alessandria) e che l’angolo alfa sottende, con il raggio R, la stessa distanza sottesa da un angolo di 9° dal raggio r della Terra e cioè la distanza tra Alessandria e l’Ellesponto.

Si ha
(2πR/360)·0.1 = (2πr/360)·9
R\r=90.

III.     DA 3D A 2D: LE PROIEZIONI E LA PROSPETTIVA

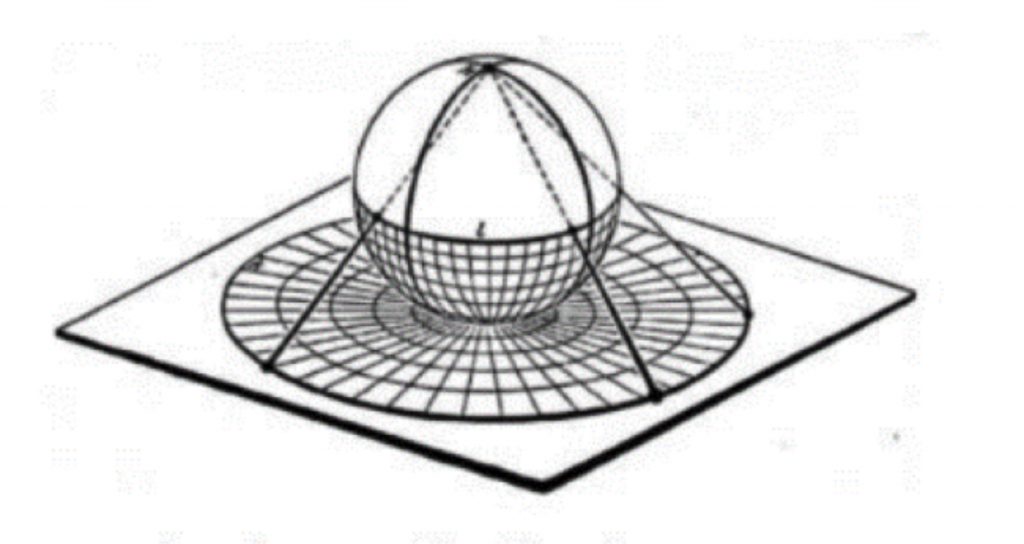
Il problema di rappresentare sul piano (2 dimensioni) lo spazio in 3 dimensioni, è per certi versi più semplice di quello di calcolare la 3° dimensione da due o più immagini in 2D, come avviene nella visione umana e si può modellare con la moltiplicazione di ogni punto S di interesse nello spazio per una matrice opportuna il cui risultato è un punto P nel piano. I coefficienti della matrice dipendono dal tipo di proiezione che si vuole ottenere. Questa operazione è nota dalla nascita della cartografia che ha come autorevoli mentori Ipparco (II sec. a.c.) e l’ingegnere romano Vitruvio (I sec. a.c.) e numerosi approfondimenti sono seguiti fino agli studi sulla prospettiva nell’ambito delle arti.

Di questi ultimi ricordiamo in particolare quello di Guidobaldo Del Monte o Guidubaldo Bourbon Del Monte (Pesaro, 11 gennaio 1545 – Mombaroccio, 6 gennaio 1607) è stato un matematico, filosofo, astronomo e marchese italiano. Guidobaldo scrisse un importante libro sulla prospettiva, intitolato Perspectivae Libri VI, pubblicato a Pesaro nel 1600, che avrà ampia diffusione negli anni successivi. Fu sicuramente, anche secondo il parere dell’amico Galileo, uno dei massimi studiosi di meccanica e matematica del Cinquecento.

IV.        DA 2D A 3D: RICOSTRUIRE LA PROFONDITÀ DALLA VISIONE STEREOSCOPICA

Sul fronte opposto, ci si è posti il problema di rilevare una terza dimensione da 2 o più immagini bidimensionali (multiple view geometry) Per rilevare il monte Pilatus, Cappeler lo ha osservato, attraverso due lastre uguali, piane e trasparenti, distanti tra di loro di una lunghezza b detta base. Su di esse ha tracciato un sistema di riferimento cartesiano ortogonale e, sulle perpendicolari condotte dall’origine, ha scelto due punti O1 e O2 posti, dalle rispettive lastre, ad una distanza c detta distanza principale

Nota la geometria del sistema di riferimento (b e c) e la disparità (x1’, x2′) siamo in grado di ricavare la profondità cioè il segmento da P’ perpendicolare a O1O2

V.            ANALIZZARE LE IMMAGINI: I CONTORNI

Un notevole problema che si presenta nel riconoscimento delle immagini, è evidenziare i contorni. Nel passaggio dall’interno all’esterno di una immagine (contorno) si ha una variazione del colore o della luminosità, e nel dominio della frequenza si ha una frequeza “alta”. Un metodo che produce impressionanti risultati è l’applicazione di un filtro passa-alto alla trasformata di Fourier bidimensionale dell’immagine.  Jean Baptiste Joseph Fourier nacque ad Auxerre, Francia nel 1768, famoso per il suo lavoro “La Théorie Analitique de la Chaleur” pubblicato in 1822 e Tradotto in inglese nel 1878: “Teoria analitica del calore “. Nessuno prestò molta attenzione al primo lavoro pubblicato: una delle più importanti teorie matematiche in ingegneria moderna [FOUR]. Qui sotto la trasformata discreta di una funzione f(x,y) e la antitrasformata. 

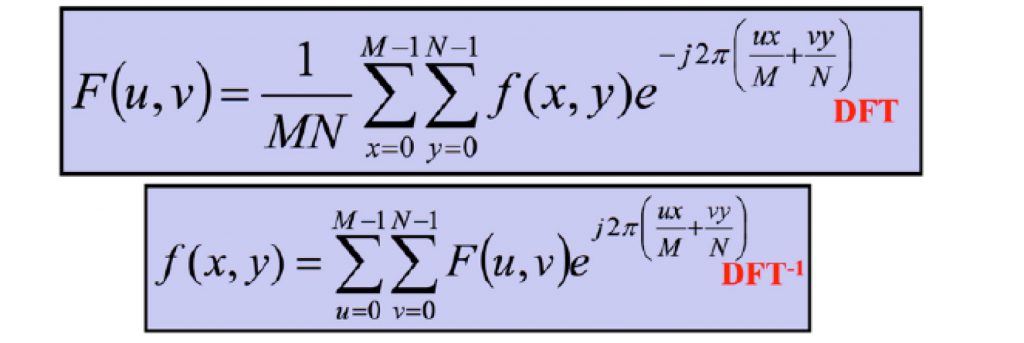
La trasformata di Fourier ha infatti molteplici applicazioni nel trattamento e filtraggio dei segnali, come si vede dalla figura sotto: l’esaltazione dei contorni è ottenuta trasformando l’immagine con la formula di Fourier, poi riducendo le componenti di bassa frequenza dell’immagine così trasformata con un filtro passa-alto. 

Un’operazione collegata alla trasformazione di Fourier è l’operazione di convoluzione: in una dimensione consiste nel calcolare la superficie generata da tante parti che si sovrappongono via via quando una funzione f1 trasla verso una f2 che rimane “ferma”.

 La convoluzione di 2 funzioni “quadrato” dà una funzione “triangolo”.

Il teorema di convoluzione permette di utilizzare la trasformata di Fourier, per la quale può risultare più semplice operare (ad esempio per applicare un filtro passa-basso): la trasformata della convoluzione di due funzioni è uguale al prodotto delle trasformate delle singole funzioni. Ovviamente il teorema vale anche nello spazio bidimensionale, cioè per le immagini.

Se applichiamo un nucleo di convoluzione [KER]  (per semplicità ne tralasciamo qui la definizione) a una immagine, si opera un filtro che migliora la comprensione dell’immagine (il filtro scelto riduce il rumore). Questa operazione è utilizzata con un significato simile nelle reti neurali convoluzionali.

VI.        LE RETI NEURALI ARTIFICIALI E L’APPRENDIMENTO 

L’osservazione della enorme complessità di un sistema nervoso (nell’uomo si hanno circa 10^11 neuroni e 10^15 connessioni) ha portato alla progettazione di reti neuronali artificiali.  Le reti neurali artificiali, emulano il comportamento dei neuroni, che interconnessi tramite le sinapsi che trasmettono segnali di attivazione verso i neuroni adiacenti. Le reti neurali più comuni sono le feed-forward, e sono grafi aciclici.  

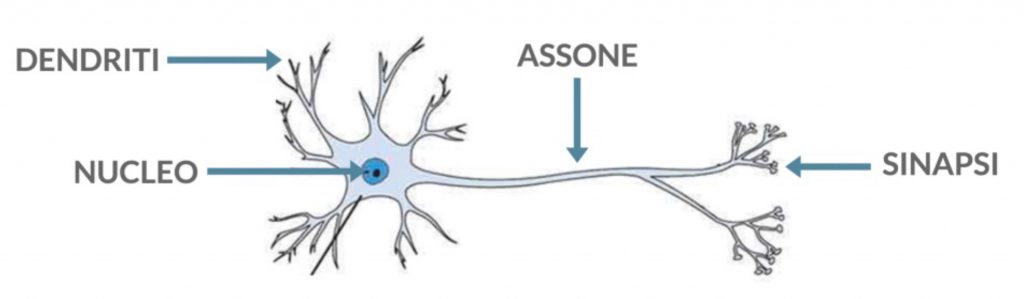
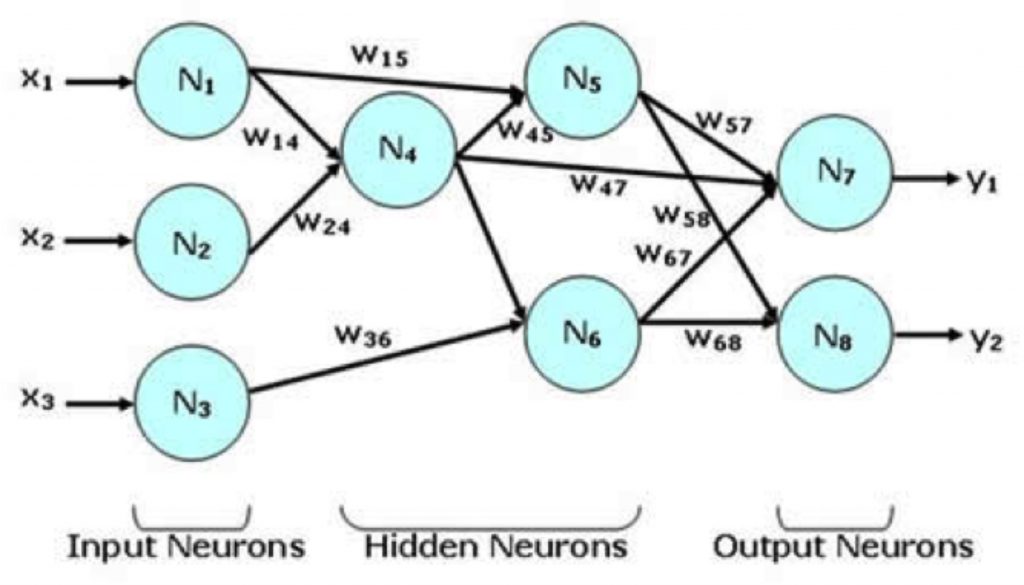
Le reti neurali artificiali (quelle che girano su un computer invece di un cervello) possono essere pensate come un modello che approssima una funzione di più input e output continui. La rete è costituita da un grafo con la topologia dei neuroni, ciascuno dei quali trasforma con una funzione (chiamata funzione di attivazione) gli ingressi trasportati sui bordi interni e invia l’output sui suoi bordi esterni. Gli ingressi e le uscite sono pesati dai pesi w_ije spostati dal fattore di polarizzazione (bias b) specifico di ciascun neurone. Ad esempio:

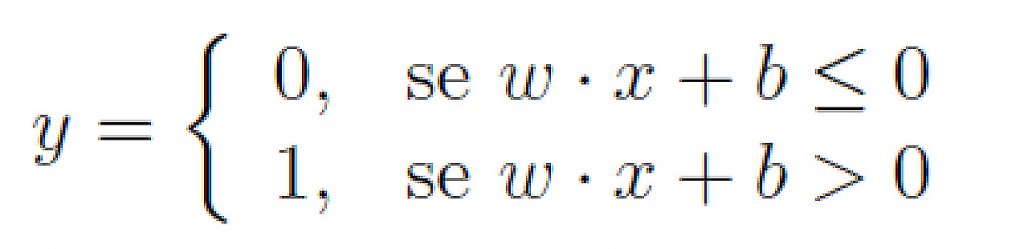
Come determino i valori dei pesi e dei bias ?

Attraverso i dati di addestramento: coppie di insiemi di ingressi e uscite, (X_{_i}, Y__i), in cui:

X__iindica l’input per tutti i neuroni di input. 

Y__iè l’output desiderato della rete neurale dopo aver eseguito gli input in X__i.

Z_i è l’insieme delle uscite della rete neurale per l’insieme degli ingressi X__i

(Nel problema del riconoscimento delle immagini, l’ingresso è una immagine e l’uscita è un valore che rappresenta la sua classificazione.)

Troviamo quindi i pesi e i bias dei neuroni nella rete che minimizzano l’errore di somma quadrata dei dati di allenamento. 

E(W) = Min Σ (Y_i– Z_i) ²
ovvero, 

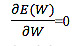
che ci riporta alla soluzione di un sistema lineare, con i cui risultati posso calcolare i pesi dell’ultimo strato e così via a ritroso fino a trovare i pesi del primo strato. 

Dalle prime reti neurali degli anni ’90, utilizzate ad esempio per il riconoscimento della scrittura, alle ultime reti neurali usate per il riconoscimento delle immagini in tempo reale, il passo non è stato breve: la disponibilità di mezzi di calcolo più potenti, ha permesso di aumentare la complessità delle reti e accrescere i dati di training, rendendo possibili le applicazioni definite come di A.I..

VII.       LE RETI NEURALI CONVOLUZIONALI

Un requisito alla base del riconoscimento è l’invarianza dell’immagine rispetto a rotazioni, traslazioni (la torre Eiffel^[1]  è sempre la stessa se vista dal basso o da un aereo!), alcuni strati delle CNN sono dedicati a questo.

I dati di addestramento e la struttura della rete neurale sono proprio finalizzati a far riconoscere alla macchina le stesse cose riprese da diversi punti di osservazione:

Per riassumere, i problemi nel riconoscimento di immagini che sono stati grandemente migliorati con gli ultimi studi e implementazioni sono:

• l’invarianza rispetto a rototraslazioni
• la sintesi delle caratteristiche uniche dell’immagine (features extraction)

Le reti neurali che hanno avuto successo dicevamo sono le CNN (Convolutional Neural Network), in quanto la convoluzione permette di ottimizzare entrambi gli aspetti sopra.

VIII.     CONSIDERAZIONI SULL’APPLICAZIONE DI ISO 25000 ALLE RETI NEURALI

In un noto studio [DEEP], una delle reti proposte ha 19 strati e 144 milioni di parametri (pesi, ecc.): l’addestramento di tali reti è basato su enormi moli di dati (immagini) di cui uno sviluppo possibile è la misura della completezza rispetto ad una soglia, cioè il numero e il tipo di immagini sufficienti perché la rete le riconosca e riconosca anche quelle simili: ad esempio: il numero, le prospettive, gli sfondi delle foto del cartello stradale nella figura 15 sono sufficienti per addestrare un veicolo a guida autonoma in modo che non scambi un qualsiasi cartello stradale per un cartello pubblicitario? Per tale misura possiamo usare la metrica per la qualità dei dati di ISO 25000? La risposta a questa ultima domanda deve essere affermativa, in quanto ISO 25000 è un framework che può essere adattato a specifiche tecnologie.

Un’altra misura di qualità ISO 25000 per l’A.I. potrebbe riguardare l’overfitting, un noto problema nel campo del machine learning, in parte dipendente dalle immagini di training, nel quale il modello si adatta eccessivamente bene ai dati usati per l’addestramento e non riesce a processare correttamente i nuovi dati, in altre parole riconosce molto bene le immagini usate per l’addestramento o simili ad esse, ma sbaglia nel riconoscere immagini meno simili.

---

References 

• [TESI] Reti neurali per filtraggio adattativo, Tesi di Laurea Ingegneria Elettronica 1991, Andrea Trenta
• [PAOL] Informatica grafica: metodi, algoritmi, programmi per il disegno automatico col calcolatore – Alberto Paoluzzi –1987
• [DEEP] Very deep convolutional networks for large-scale image recognition Karen Simonyan & Andrew Zisserman, ICLR-2015
• [FRAUN] https://www.fokus.fraunhofer.de/en/fame/workingareas/ai
• [NASA] https://www-spof.gsfc.nasa.gov/stargaze/Shipparc.htm
• [WIK] https://en.wikipedia.org/wiki/Convolution
• [KER] https://it.m.wikipedia.org/wiki/Matrice_di_convoluzione
• [ETSI] ETSI MPEG meeting 112 Varsavia, 2015
• [CAFOS] Corso visione artificiale – Samuel Rota Bulò – Ca’ Foscari
• [CDVA1] Compact Descriptors for Video Analysis: the Emerging MPEG Standard   2017   Ling-Yu Duan, Vijay Chandrasekhar, Shiqi Wang, Yihang Lou, Jie Lin, Yan Bai, Tiejun Huang, Alex Chichung Kot, Fellow, IEEE and Wen Gao, Fellow, IEEE
• [CDVA2] ISO/IEC 15938-15:2019 Information technology — Multimedia content description interface — Part 15: Compact descriptors for video analysis
• [CONVC] Convolutional Networks course https://cs231n.github.io/convolutional-networks/
• [WIK2] Metodo Cappeler -it.wikipedia.org
• [FOUR] Rafael Gonzalez, Richard Woods  -Digital Image Processing- (2002)

---

^[1] Esempio tratto da ETSI MPEG, il gruppo fondato e guidato per lungo tempo da Leonardo Chiariglione che ha dato vita al famoso codec MP3 per la musica, e l’MPEG-2 usato per la TV digitale e i DVD in tutto il mondo, che si pose nel 2005 il tema della classificazione delle immagini, ovvero la creazione di un meccanismo efficiente che consenta di ricercare e confrontare immagini in base al loro contenuto “semantico”.

---

Biografia

Andrea TRENTA, Vicepresidente Commissione Tecnica CT 504 Ingegneria del Software UNINFO-SGI, andrea.trenta@dataqualitylab.it

Andrea Trenta ha conseguito la laurea in ingegneria informatica presso l’Università di Roma La Sapienza e master in ingegneria delle telecomunicazioni presso il Ministero dell’Industria, ha più di 25 anni di esperienza in aziende leader nella standardizzazione e nei relativi processi di industrializzazione end-to-end, dal requisito all’implementazione, di apparati e sistemi IT. V.Chair di UNI CT 504 “Software Engineering”, è redattore di ISO-IEC 25030 e relatore nazionale della norma UNI TS 11725 “Linee guida per la misurazione della qualità dei dati”e membro del gruppo di lavoro per la qualità del prodotto di servizi cloud in ISO/IEC/SC7 WG6 all’interno del progetto SQUARE. Negli ultimi anni ha collaborato con l’Università dei Roma La Sapienza su protocolli di segnalazione, teoria dei giochi, e con l’università Politecnico di Torino per l’implementazione di ISO-IEC 25024 “Misurazione della qualità dei dati”.